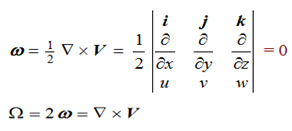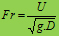Aliran Fluida

 

Klasifikasi Aliran Fluida (Fluids Flow Classification)

Didasarkan pada tinjauan tertentu, aliran fluida dapat diklasifikasikan dalam beberapa golongan. Dalam ulasan ini, fluida yang lebih banyak dibahas adalah air (incompressible fluids) dan dibagi menjadi 8 golongan antara lain :

1. Aliran yang tak termampatkan dan termampatkan (incompressible and compressible flows)
Aliran tak termampatkan adalah kondisi aliran dimana rapat massa fluidanya tidak berubah. Contohnya adalah air,minyak,dll.
Aliran termampatkan adalah kondisi aliran dimana rapat massa fluidanya berubah. Contohnya adalah gas. Pada fluida jenis ini berlaku hukum termodinamika.

2. Aliran tunak dan tak tunak (steady and unsteady flows )

Aliran tunak atau aliran permanen (permanent flow) adalah kondisi dimana komponen aliran tidak berubah terhadap waktu. Contohnya adalah aliran di saluran/sungai pada kondisi tidak ada perubahan aliran (tidak ada hujan, tidak banjir, dll). Kondisi tersebut dinyatakan dalam persamaan matematika berikut :

jf : perubahan komponen aliran

jt : perubahan terhadap waktu

f : komponen aliran (viskositas, tekanan, rapat massa, kedalaman, debit, dll.)

Aliran tak tunak atau aliran tidak permanen (impermanent flow) adalah kondisi dimana komponen aliran berubah terhadap waktu. Contoh aliran di saluran/sungai pada kondisi ada perubahan aliran (ada hujan, ada banjir, dll) atau aliran yang dipengaruhi muka air pasang-surut (muara sungai di laut) . Kondisi tersebut dinyatakan dalam persamaan matematika berikut :

Ilustrasi visual untuk kasus sederhana ditampilkan pada gambar di bawah ini

3. Aliran seragam dan tak seragam (uniform and non-uniform flows)

Aliran seragam adalah kondisi dimana komponen aliran tidak berubah terhadap jarak. Contoh aliran di saluran/sungai pada kondisi tidak ada pengaruh pembendungan/terjunan, tidak ada penyempitan/pelebaran yang ekstrim.

jx : perubahan terhadap jarak

Aliran tidak seragam (non-uniform flow) adalah kondisi dimana komponen aliran berubah terhadap jarak. Contoh aliran di saluran/sungai pada kondisi ada pengaruh pembendungan/terjunan, ada penyempitan/pelebaran yang ekstrim.

Ilustrasi visual untuk kasus sederhana ditampilkan pada gambar di bawah ini, (a) untuk kondisi aliran seragam dan (b) untuk kondisi aliran tidak seragam

(McDonough, 2009:32)

4. Aliran laminer dan turbulen (laminar and turbulent flows)

(McDonough,

2009:38)

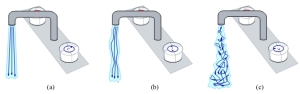
Fenomena aliran jenis ini dapat dijumpai  dalam kehidupan sehari hari, aliran air pada keran mungkin yang paling sering kita jumpai. Gambar diatas menunjukkan, Gambar (a) adalah keran air yang dibuka saat awal (bukaan kecil) sehingga air yang mengalir kecepatannya kecil, pada kondisi ini terjadi aliran laminer. Kecepata air meningkat pada Gambar (b) dan Gambar (c) sehingga aliran air berubah menjadi turbulen.
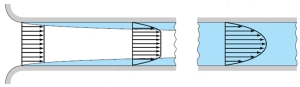
Dari sudut pandang hidraulik, hal yang paling mudah untuk membedakannya adalah gerak partikel/distribusi kecepatannya seragam, lurus, dan sejajar untuk aliran laminer dan sebaliknya untuk aliran turbulen. Perubahan dari laminer menuju turbulen atau zona transisi terjadi pada jarak tertentu dan zona transisi akan berakhir hingga terjadi kondisi ‘fully developed turbulence’. Gambar dibawah ini mendeskripsikan perubahan distribusi kecepatan pada saluran terbuka, Gambar (a) dan saluran tertutup, Gambar (b)

 
(Yulistiyanto)
(a)

 
(Kironoto)
(b)

Angka Reynolds biasanya digunakan untuk mempermudah dalam membedakan jenis aliran pada klasifikasi ini. Persamaan Reynolds untuk mendapatkan Angka Reynolds dinyatakan dalam persamaan dibawah ini :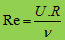
U     : kecepatan rerata tampang
R     : jari jari hidraulik (saluran terbuka); digunakan diameter (D) untuk aliran dalam pipa (saluran tertutup)
u     : kekentalan fluida (viskositas kinematik)
Setelah mendapatkan Angka Reynolds, jenis aliran dapat diketahui melalui rentang berikut,
Aliran terbuka
Re < 2000, laminer
Re > 12500, turbulen
Aliran tertutup
Re < 500, laminer
Re > 4000, turbulen
diantara rentang diatas merupakan kondisi transisi. Pada kondisi aliran laminer, pengaruh viskositas lebih besar daripada inersia dan kondisi sebaliknya untuk aliran turbulen.

5. Aliran yang dipengaruhi kekentalan dan tidak (viscous and inviscid flows)
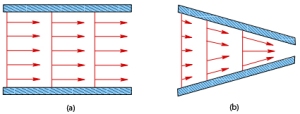
Aliran viskous atau aliran fluida nyata adalah aliran yang dipengaruhi oleh viskositas. Adanya viskositas menyebabkan adanya tegangan geser dan kehilangan energy. Pada aliran ini terjadi gesekan antarai fluida dengan dasar/dinding saluran atau pipa. Gambar (a) dibawah ini menampilkan percobaan aliran viskous melalui sebuah pilar berbentuk tabung.

(Yulistiyanto)
(a)

Aliran invisid atau aliran fluida ideal adalah aliran yang tidak dipengaruhi viskositas/kekentalan  sehingga aliran ini tidak memiliki tegangan geser dan kehilangan energi. Dalam kenyataannya aliran fluida ideal tidak ada. Konsep ini digunakan para peneliti terdahulu untuk membentuk persamaan aliran fluida dan pengaplikasiannya di lapangan ditambahkan faktor penyesuaian sesuai kondisi nyata. Gambar (b) dibawah ini mengilustrasikan aliran invisid melalui sebuah pilar berbentuk tabung.

(Yulistiyanto)
(b)

6. Aliran rotasi dan tak rotasi (rotational and irrotational flows)
Aliran irrotasional adalah aliran dimana nilai rotasinya atau setiap komponen vektor rotasinya sama dengan nol. Contoh aliran irrotasional adalah medan aliran pada aliran seragam. Penjabaran matematisnya disajikan pada pesamaan berikut

Omega (kapital) sering dinotasikan sebagai vortisitas (vorticity), sehingga didefinisikan sebagai sebuah vektor yang nilainya dua kalinya vektor rotasi.
Sedangkan aliran rotasional adalah aliran dimana nilai rotasinya atau setiap komponen vektor rotasinya tidak sama dengan nol. Hal ini berarti medan aliran dengan kecepatan vektor V atau curl V tidak sama dengan nol. Contoh  dari aliran rotasional ditampilkan pada Gambar (a), tampak terjadi pusaran/vortex yang disebabkan ketidakseragaman aliran oleh perubahan penampang akibat terjunan. Namun jauh dari terjunan, aliran masih seragam sehingga aliran irrotasional.

(McDonough, 2009:34)
(a)

7. Aliran subkritis dan superkritis (subcritical and supercritical flows)
Untuk membedakan jenis aliran pada klasifikasi ini sering digunakanAngka Froude. Angka Froude diperoleh melalui persamaan dibawah ini dan merupakan bilangan tak berdimensi,

U     : kecepatan rerata tampang

g      : percepatan gravitasi

D     : kedalaman aliran

penyebut pada persamaan diatas merupakan persamaan dari kecepatan rambat gelombang (celerity). Setelah mendapatkan Angka Froude, penentuan jenis aliran melalui rentang berikut,

F < 1, aliran sub-kritik

F > 1, aliran super-kritik

F = 1, aliran kritik

8. Aliran yang terpisahkan/separasi dan tidak (separated and unseparated flows)
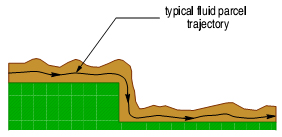
Aliran yang tidak terjadi separasi dapat terjadi pada aliran yang sangat lambat. Penjelasan mengenai fenomena ini ditampilkan melalui sketsa pada Gambar (a), mengilustrasikan sebuah percobaan sejumlah cairan sirup (viskositas tinggi) dengan suhu rendah yang melampaui flume dengan beda tinggi  dasar tertentu dengan kecepatan sangat rendah. Saat mencapai pojok flume, cairan sirup tetap megikuti dasar flume, turun vertical dan tetap ‘menempel’ hingga akhir. Fenomena ini disebabkan momentum yang sangat kecil pada pojok dasar flume yang diakibatkan kecepatan yang sangat rendah.

(McDonough, 2009:40)
(a)

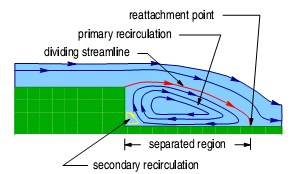
Sedangkan aliran yang terjadi separasi ditampilkan sketsa pada Gambar (b). Fluida dengan nilai viskositas kecil atau kecepatan tinggi menimbulkan momentum yang tinggi, sehingga sulit bagi aliran untuk ‘menempel’ pada dasar saluran. Pada Gambar (b) juga mengilustrasikan aliran rotasional yang telah dijelaskan sebelumnya.

(McDonough, 2009:40)
(b)

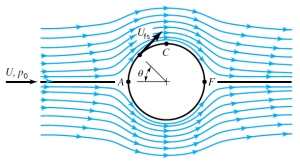
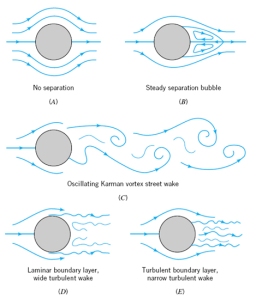
Gambar (c) dibawah ini juga mengilustrasikan fenomena aliran pada klasifikasi ini. Pada bagian Gamabr (A) dan Gambar (B) juga mengilustrasikan fenomena aliran viscous dan non-viskous di penjelasan sebelumnya.

(Yulistiyanto)
(c)

 

May be useful for you

Sumber :
McDonough, J. M., 2009. Lectures in Elementary Fluid Dynamics : Physics, Mathematics and Application. Lecture Notes. Lexington : Departments of Mechanical Engineering and Mathematics, University of Kentucky

Kironoto, Bambang Agus. Hidraulika-Klasifikasi Aliran. Diktat Perkuliahan. Jogjakarta : Universitas Gadjah Mada

Yulistiyanto, Bambang. 2012. Mekanika Kontinum-Boundary Layer. Diktat Perkuliahan. Jogjakarta : Universitas Gadjah Mada

Sumber Advertisements